二元一次方程式 ax+by=cをグラフで表す問題です。 解き方 x=0 y=0 など適当な数字を代入して 2点の座標を求めて 2点を直線で結ぶ。 ポイント 切片が分数になる場合は2の方法を使った方が正確なグラフが書けます。 x軸、y軸に平行なグラフ一次方程式y=1/2x-2 に実際に任意の何らかの値を入れてグラフを描く方法もあります。 例えば、x=0 のとき一次方程式にx=0を代入するとy=2となります。よって、このグラフは、座標(0, 2)を通ることが分かります。次の中から右上がりのグラフになる式をすべて選び記号で答えよ。 ア) y=3x5 イ) y=x12 ウ) y=5x8 エ) y= 2 7 x1 オ) y= 3 5 x5 y=3x1のグラフと平行なグラフの式を選んで記号で答えよ。
1
一次方程式 グラフ excel
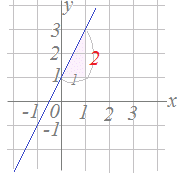
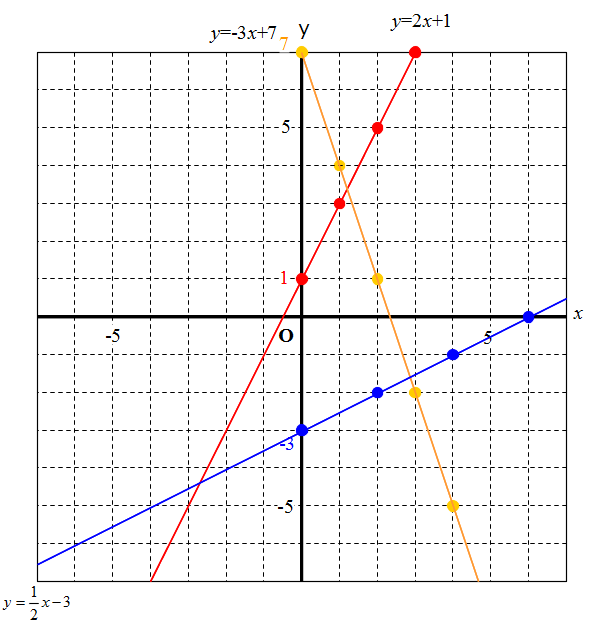
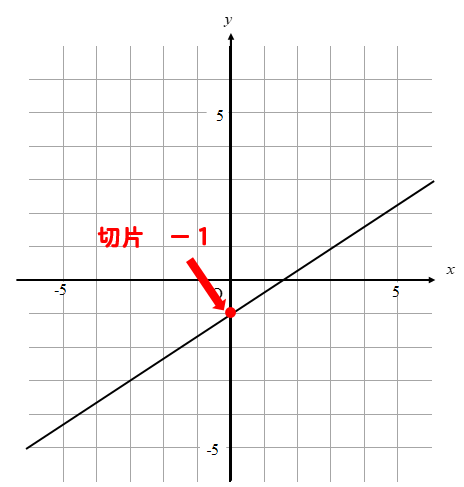
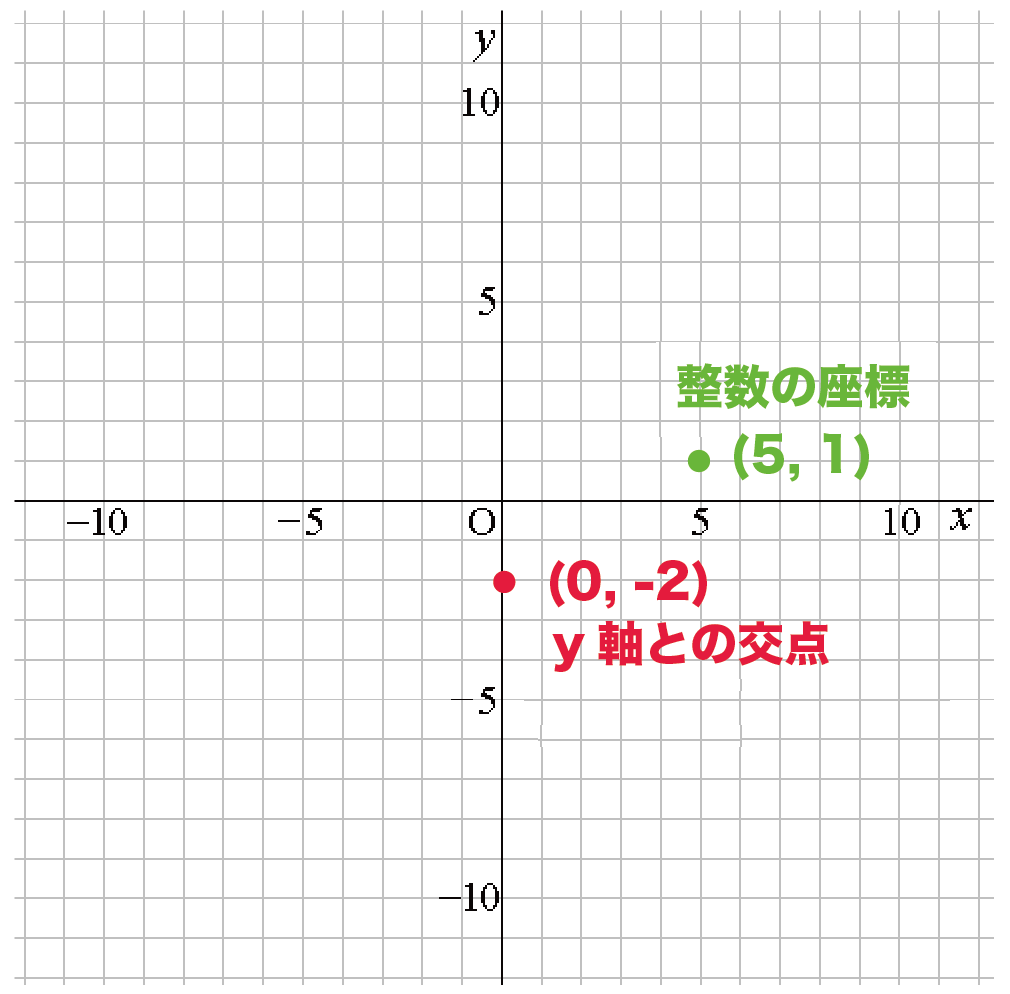
一次方程式 グラフ excel-1次関数 y= a xb のグラフの傾きは a ,切片は b です. (1) 切片 は, y 軸との交点(の y 座標)という「目に見えるもの」なので,切片の意味を間違う生徒は少ないです. 右の図は y=2x1 の直線のグラフで,その切片は赤丸で示した y 軸との交点の y 座標, 1 です. (2) これに対して 傾き は, y= の形に書いたときの x の係数ですが,その図形的な意味が分からない Excel。y=2x。一次元方程式のグラフの作り方。 グラフ Excelの研修講座で、先日ご質問があったものの中に、 「一次元方程式のグラフがうまく作れない」 ので、困っているといわれまして。 確かに、通常のようなグラフの作り方では、うまく作ることが出来ないんで



1次関数 グラフ 直線の方程式
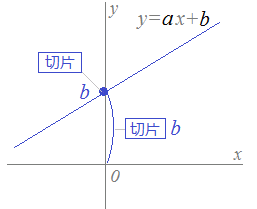
一次方程式 グラフ 傾き 4 aが傾きだ, >直線Lのグラフが、直線ABとx軸上で交わるとき、直線Lの傾きを求めなさい。 =x2y10 問題1 次の直線は,切片の値が である直線のグラフです. 傾きは,はじめ1に設定されていますが,マウスを直線に近付けると傾き1次関数のグラフを見て,方程式が答えられるようにする. I 直線のグラフから「 切片 」と「 傾き 」を読み取れるようにする. II 直線のグラフから 1次関数の方程式 を答えられるようにする. III 傾きが分数になるとき でも,直線のグラフから1次関数の方程式を答えられるようにする. (1) 定数項 b は「 切片 」と呼ばれます. •切片 b は,次の図2のように y 軸 最近中学で一次方程式のグラフをやっていて「これPythonにやってもらえれば楽できる面白いじゃん」と思って作ることにしました。 仕様 変化の割合(傾き)と切片を入力するとグラフが表示される。 変化の割合が分数にしたい場合はy/xのような形で入力する。
③二元一次方程式と一次関 数の関係に関心をもち, 二元一次方程式の解と一 次関数のグラフの関係に ついて考えようとしてい る。 ④具体的な事象から取り出 した2つの数量の関係に ついて,自ら課題を見い だし,その課題解決のた めに他者の考えも踏まえエ 一次関数のグラフと二元一次方程式のグラフとの関係や連立方程式の解とグラフとの関係を明らかに する。 オ 具体的な事象を一次関数とみなし,それを問題解決に利用できるようにする。 5 単元の指導計画 1.一次関数とグラフ(10時間)連立方程式 中学数学2元1次方程式と連立方程式 中学数学連立方程式・加減法 中学数学連立方程式・代入法 中学数学連立方程式 小数・分数;
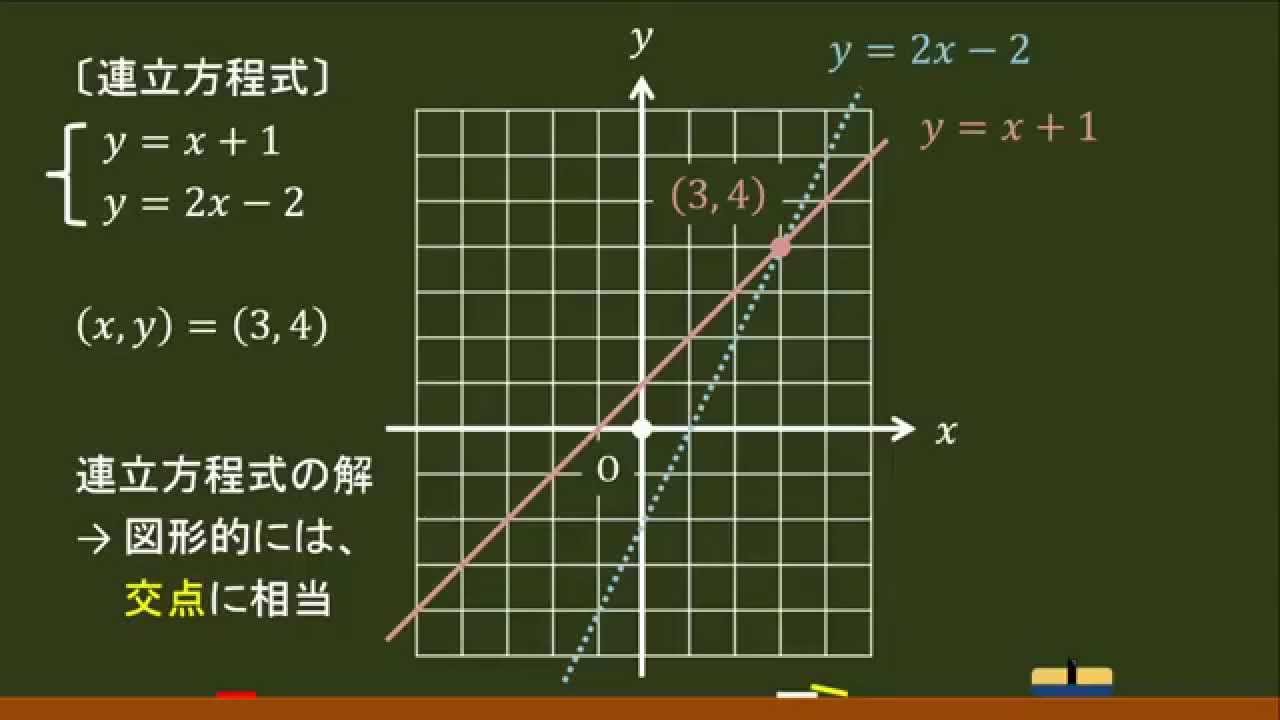
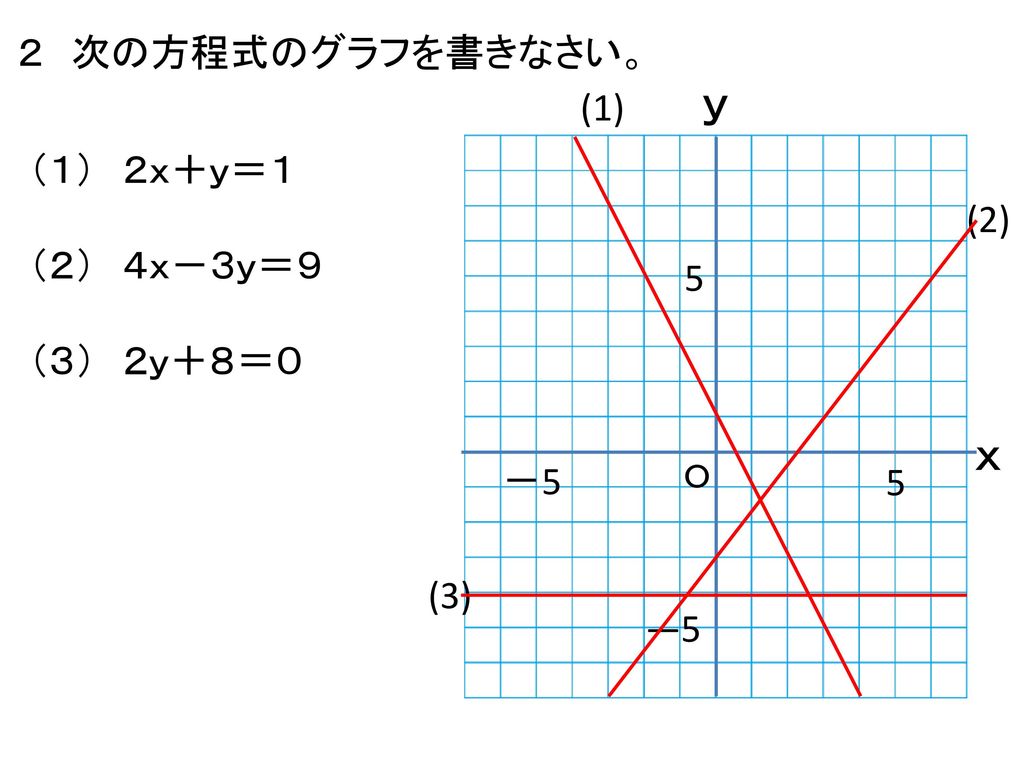
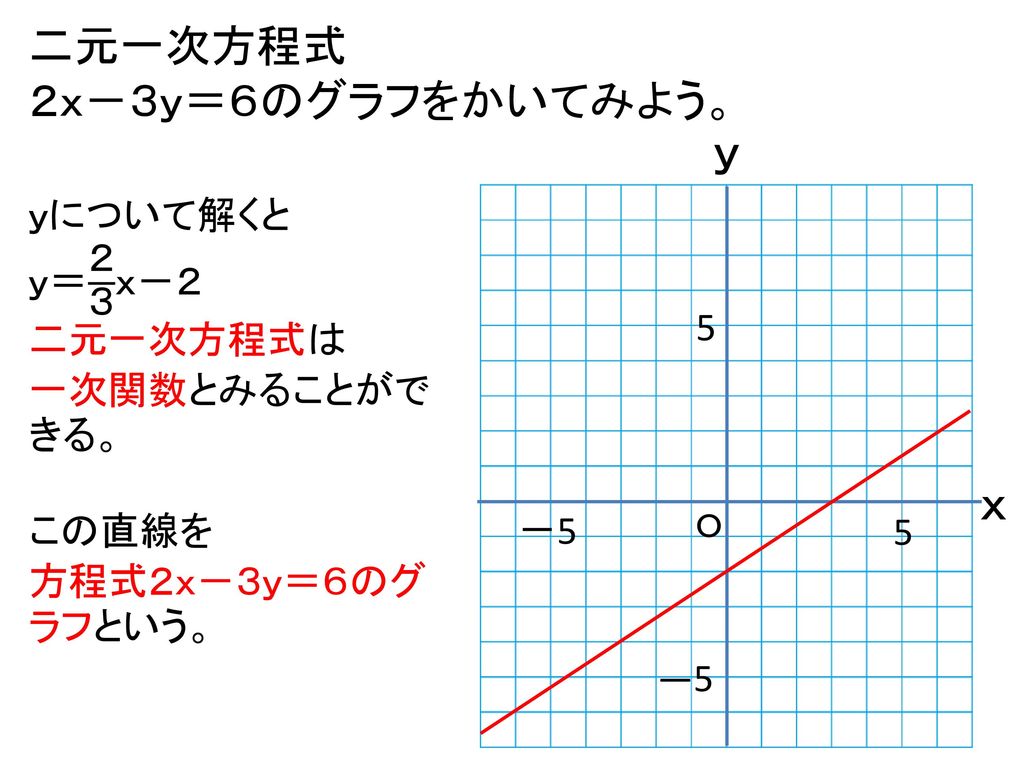
方程式と一次関数のグラフの関係 ①連立方程式とグラフの関係 連立方程式 axb=c dxe=f においてその解(m,n)と、一次関数axb=c,dxe=fの それぞれのグラフの直線の交点の座標(m',n')において (m,n)と(m',n')は一致する。 ちょっと難しそうに聞こえるが、例を挙げよう。<二元一次方程式のグラフの書き方> Ⅰy =ax +b の形に変形し, 一次関数の傾きと切片を利用して書く。 Ⅱグラフが通る点を2点以上見つけて書く。 (x,y ともに整数値が良い) (※)x =0 とy =0 を代入すると求めやすい つまりx 軸とy 軸との交点の座標を求めると良い2数_一次関数_二元一次方程式のグラフ 数学中235 二元一次方程式のグラフを書く Duration 926 とある男が授業をしてみた 249,776 views 926 2数 一次関数 変域の求め方 2元1次方程式のグラフが直線であ ることを理解させる。




中2数学 二元一次方程式 証明 中学生 数学のノート Clear
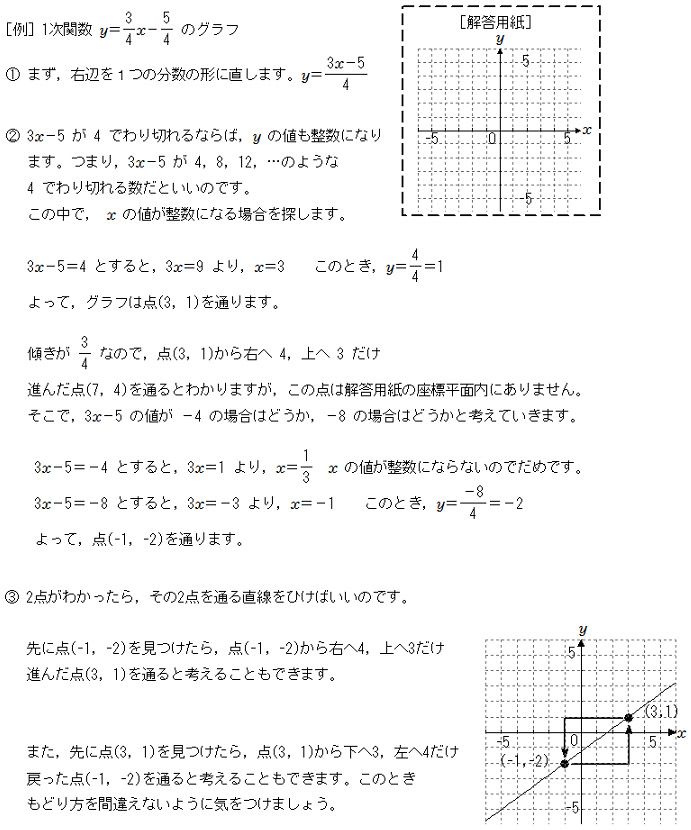



1次関数 傾きや切片が分数であるグラフのかき方 中学数学 定期テスト対策サイト
求めよ、と指示されているのは直線の式です。 つまり、 y =axb y = a x b の形で答えなくてはなりませんね。 よって、 y = 3 4x 1 4 y = 3 4 x 1 4 スポンサーリンク 次のページ 一次関数・式の決定 前のページ 一次関数・式からグラフへ一次関数のグラフを作成する topへ 一次関数の y=axb というグラフを作成してみたいと思います。 データリストを作成すします。 定数の a と b を変更することができるように、下図のようなデータリストを作成しました。エクセルで一次方程式を計算し、グラフを書く方法 まず、一次関数とは、y = ax b という式で表されるものです。 これをエクセル上で表し、グラフにしていきましょう。今回はy=5x2という一次方程式を描いていきましょう。




1次方程式と1次関数 数学i フリー教材開発コミュニティ Ftext



1次関数 グラフ 直線の方程式
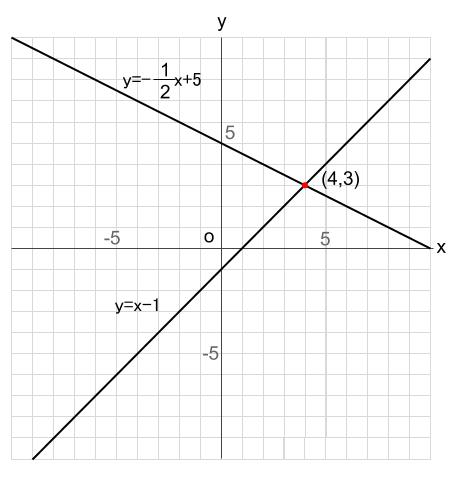
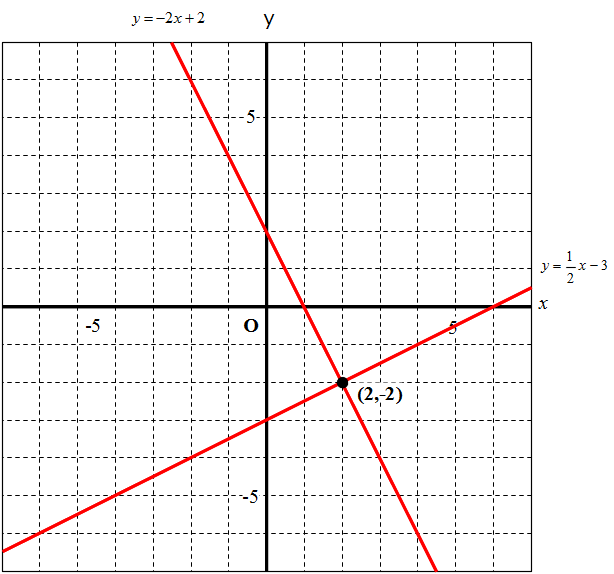
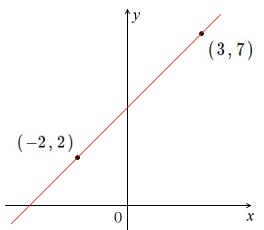
1次関数のグラフを見て,方程式が答えられるようにする. i 直線のグラフから「切片」と「傾き」を読み取れるようにする. ii 直線のグラフから1次関数の方程式を答えられるようにする. グラフから交点を読み取る! グラフの交点が、それが連立方程式の解となるので、解は (x、y)=(1、2) ・・・(答え) はい、次の問題 中2数学:一次関数と方程式(2直線の交点の座標の求め方) 中2数学:一次関数と方程式(2直線の交点の座標の >グラフが2点(14) (2,6) を通る1次関数について グラフの傾きを求めなさい。 どのようにして解けば良いですか? 連立方程式を使うのがいいね。 y=axbに2つの座標のxとyを代入してaとbの連立方程式を作ってみよう



中学数学 連立方程式 二元一次



1
単元「一次関数」の小単元「連立方程式とグラフ」(2時間)における数学的活動を取り入れた授業モデルです。 下の授業展開案を授業にご活用ください。 単元 一次関数 (啓林館) 2 一次関数と方程式一次方程式axby-z=-cが表す平面、(a, b,-1) を法線ベクトルとする平面 に他ならない。 ・以上から、z= axbycのグラフとは、 (a, b,-1) を法線ベクトルとする平面であることがわかる。 2 2変数1次関数z= a (x-x 0) b (y-y 0) z 0 のグラフは、一次関数のグラフ(式の求め方) 一次関数 と方程式 連立方程式 とグラフ 一次関数の利用1 一次関数の利用2(動点の問題) 二学期中間テスト 定期テスト(中間・期末・学年末)の問題用紙と解答用紙 図形




Bar13 Z 2y8 Descubre Como Resolverlo En Qanda



中2 1次関数4
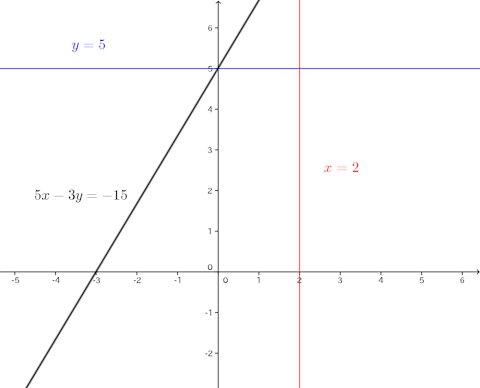
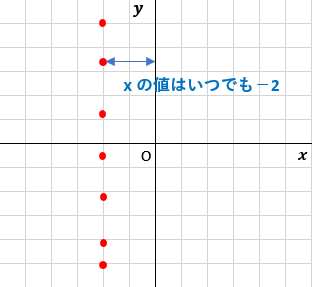
1 二元一次方程式のグラフ a,b,cを定数とすると,二元一次方程式 axby=c のグラフは直線である。 2 y=k,x=h のグラフ ⑴ y=k のグラフは,x軸に平行な直線である。 ⑵ x=h のグラフは,y軸に平行な直線である。 3 連立方程式とグラフ2年生 3 一次関数 問題6 二元一次方程式と一次関数のグラフとの関係 二元一次方程式ax +by +c =0で,x の値が1つ決まれば,それに対応するy の値がただ1つ決まることから,この式をy がx の一次関数であることを表す式 とみることができるよう指導することが大切である。グラフの傾きが 3 で、点 (2, 5) を通る一次関数を求めなさい。 解答 式を作ることは、とっても簡単です! 一次関数の問題を解くポイントは方程式の理解とグラフを図示する力です。
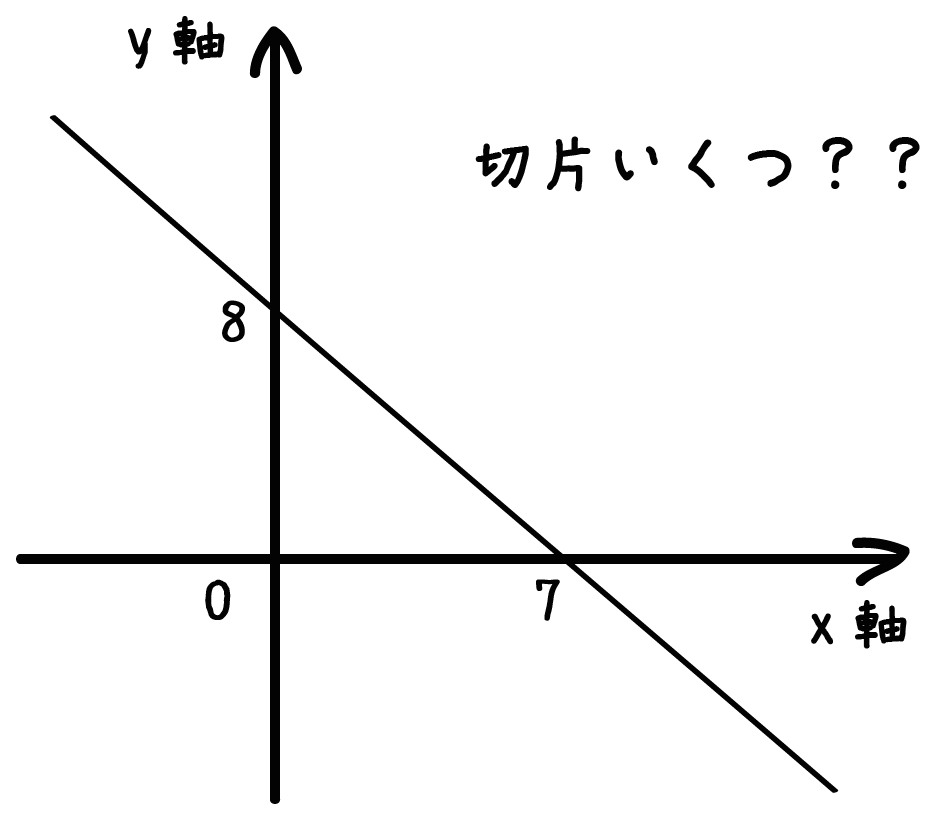



中2数学 一次関数の切片を求める2つの方法 Qikeru 学びを楽しくわかりやすく



1
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru(知:学習プリント) ・連立方程式の解とグラフの関係が理解できる。 (考:学習プリント) 2 ② 3 二元一次方程式と一次関数の関係を調べる。 (1)二元一次方程式の解の組を座標平面上に表す。 (2)連立方程式とグラフの関係を調べる。1次関数の交点の座標とグラフから直線の方程式を求める方法 中学2年 1次関数 1次関数との交点の座標の求め方と、グラフから読み取り直線の方程式を求める方法です。 ここでは1次関数に限定して直線と直線の交点を求める問題を取り上げて説明します。 交点を求める問題は1次関数だけでなく高校の数学でも必ず必要になりますが、考え方はすべて同じです。
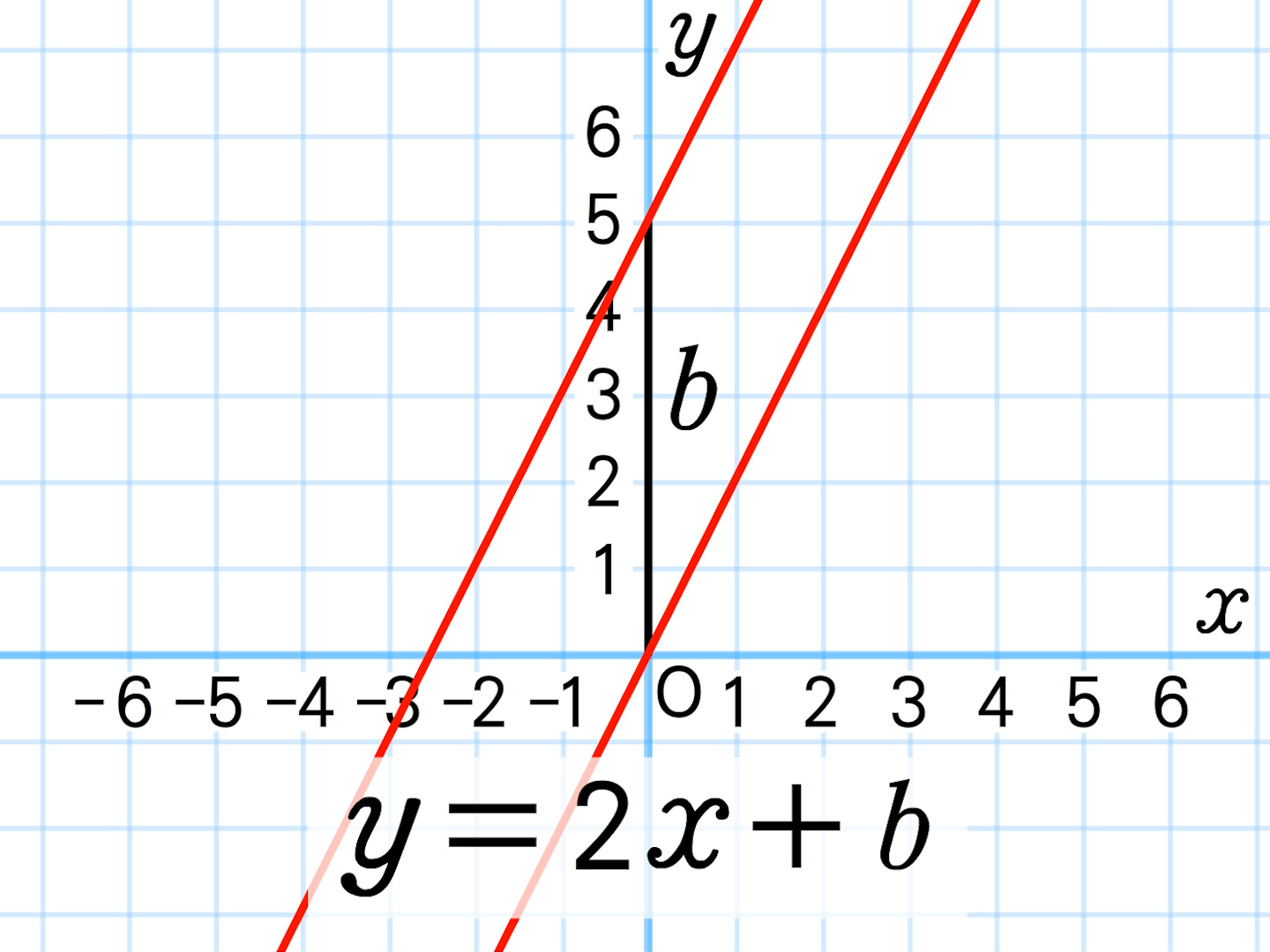



2年 1次関数のグラフ 1 数学イメージ動画集 大日本図書
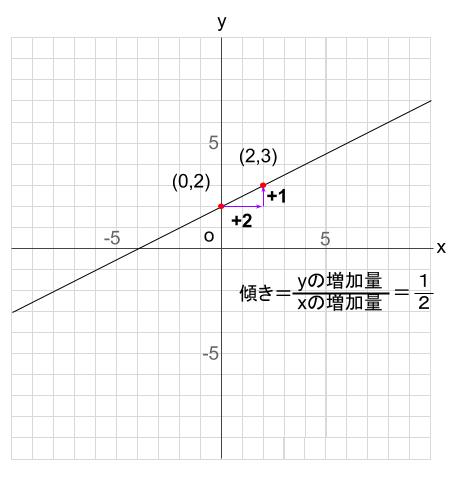



中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su
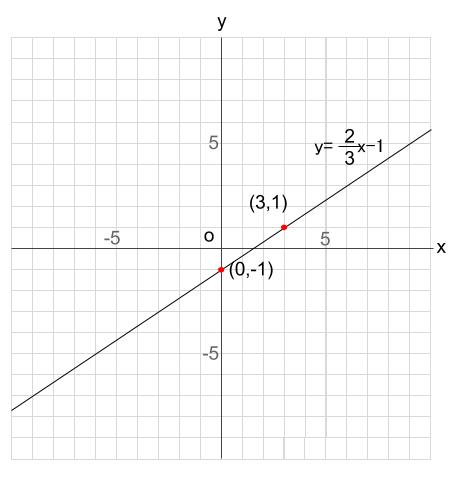
平成21年度 中学校 数学a (12) 二元一次方程式のグラフ (pdf:150kb) 2年 平成24年度 中学校 数学a (13) 二元一次方程式の解とグラフ (pdf:179kb) 2年 平成30年度 中学校 数学a (13) 二元一次方程式と一次関数のグラフの関係 (pdf:kb)2方程式と一次関数4・二元一次方程式のグラフの意味や連立方程式の解と 本時グラフとの関係を理解する。 ()2/4 33章のまとめ1・一次関数の意味、変化の割合、一次関数のグラフ、 直線の式の求め方、二元一次方程式とグラフのまとめ をする。一次関数のグラフの書き方 まとめ それでは、最後にグラフの書き方をおさらいしておきましょう。 グラフの書き方の手順は以下の通りでしたね。 傾きと切片を読み取る;
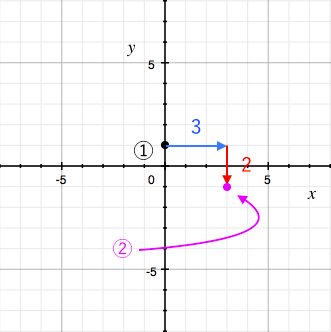



一次関数 グラフの書き方 苦手な数学を簡単に




一次関数はこれで完璧 グラフの書き方と変化の割合の求め方
が、関数的表現を用いて二元一次方程式の解を表し、グラフで表現する際 には離散的なグラフであると捉えてしまう生徒の実態を予想することがで きる。 2.二元一次方程式と一次関数の関係



1次関数 グラフから直線の式を求める 勉強ナビゲーター




一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download



Studydoctor2元1次方程式とグラフの書き方 中2数学 Studydoctor



Math 超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 働きアリ
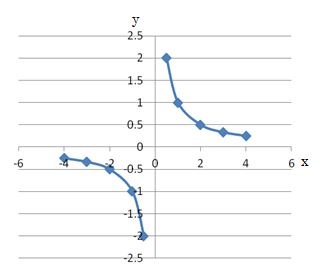



1次関数 方程式 のグラフ もう一度やり直しの算数 数学




中2数学の二限一次方程式グラフです 書き方がわかりません 教えてください Clear




Excel エクセルで一次関数を計算し グラフを作る方法 一次関数の解を求める方法




方程式とグラフ 無料で使える中学学習プリント




一次関数の傾きと切片を求める問題 Irohabook
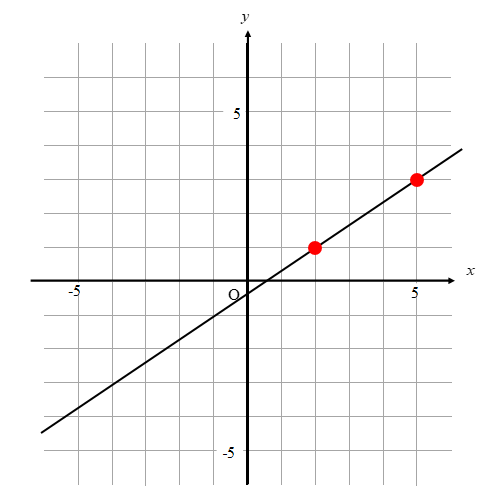



一次関数のグラフ 傾き 切片が分数 グラフの書き方を徹底解説 数スタ



一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス



一次関数のグラフ 中学2年 数学クラブ
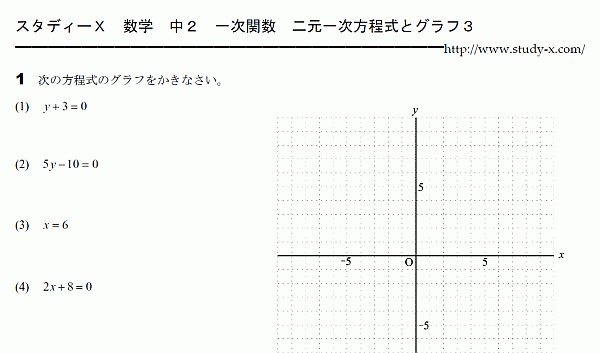



二元一次方程式とグラフ その3 無料学習プリント教材
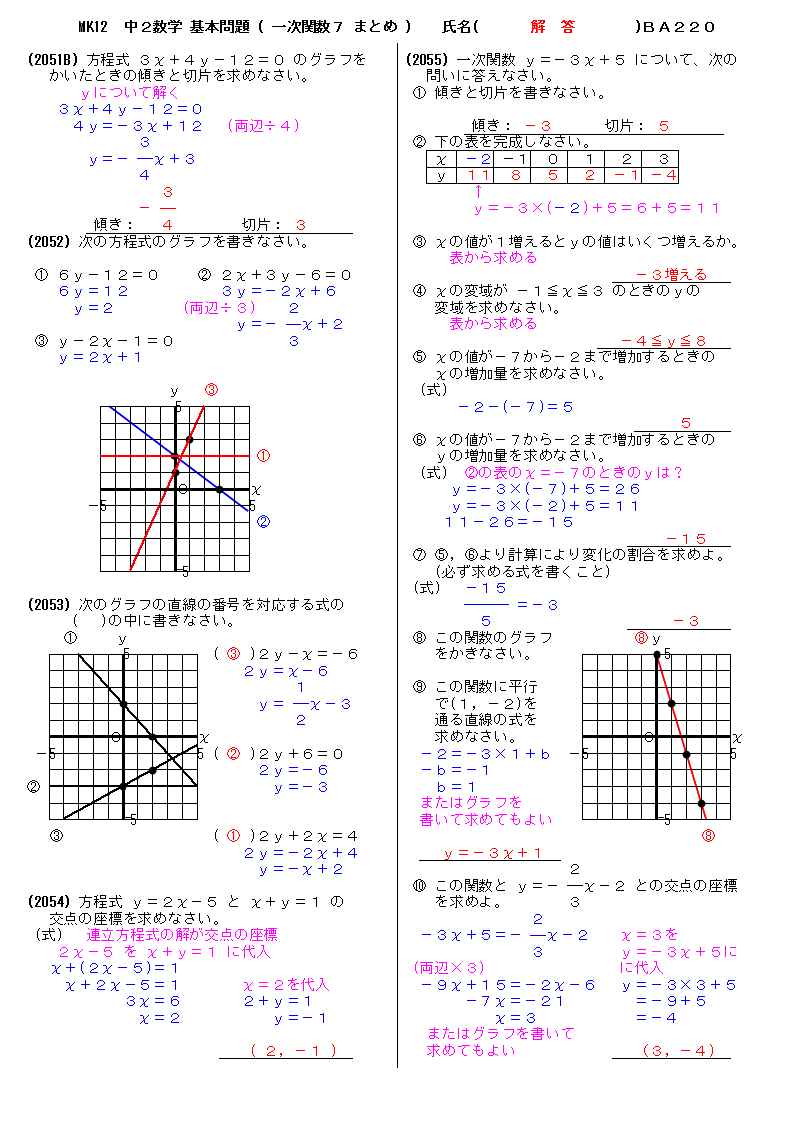



無料 中2数学 基本問題 解答プリント 2 一次関数7 まとめ




1次関数 グラフ 直線の方程式
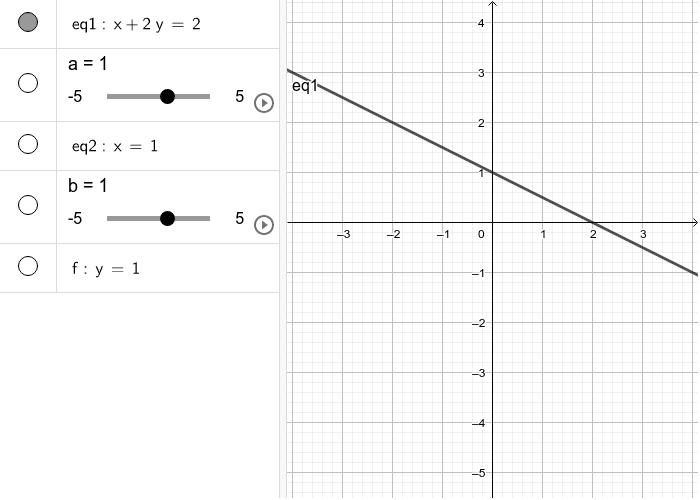



1次関数と方程式 Geogebra




一次関数の問題の解き方 7パターン 数学fun




切片とは 超簡単 切片を一瞬で求める方法 傾きとの違い 高校生向け受験応援メディア 受験のミカタ
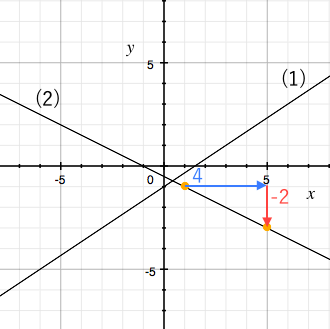



一次関数 グラフから関数の式を答える 苦手な数学を簡単に




不定方程式とは 基礎知識と解き方を解説 高校生向け受験応援メディア 受験のミカタ




一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典
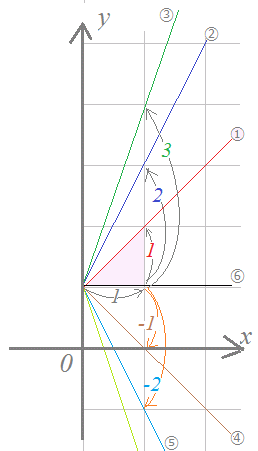



1次関数 グラフ 直線の方程式



ねこ騙し数学
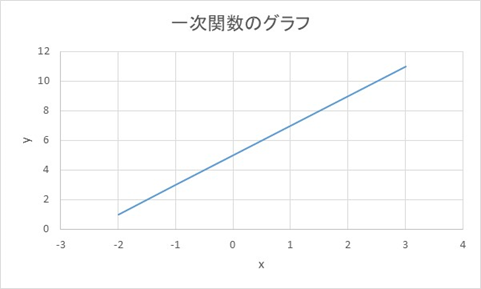



Excel エクセルにて1次関数 一次方程式 の計算 解や傾き とグラフ化の方法 複数も More E Life



2




バカでもわかる 中学数学 1次関数




一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 リョースケ大学
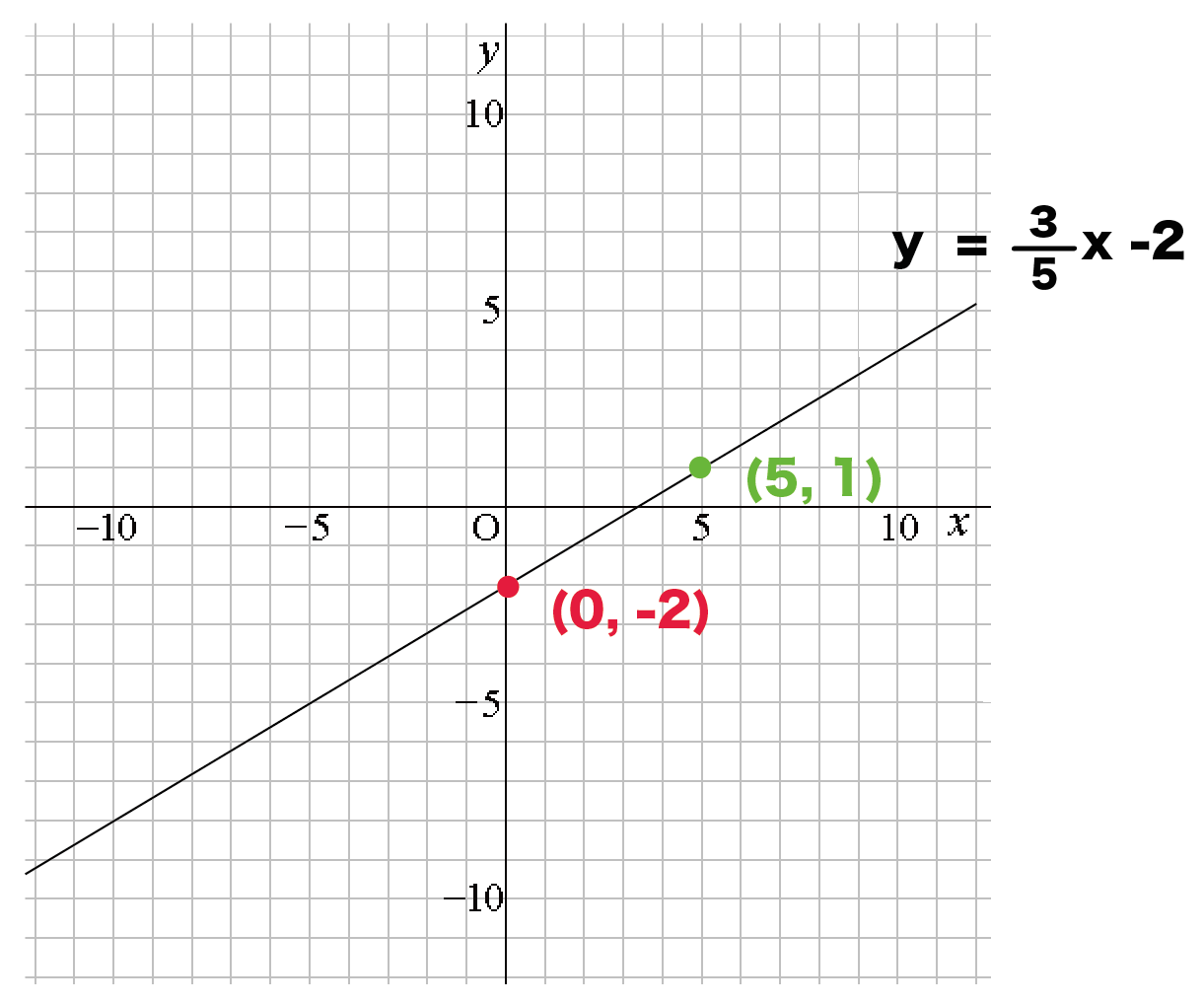



中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
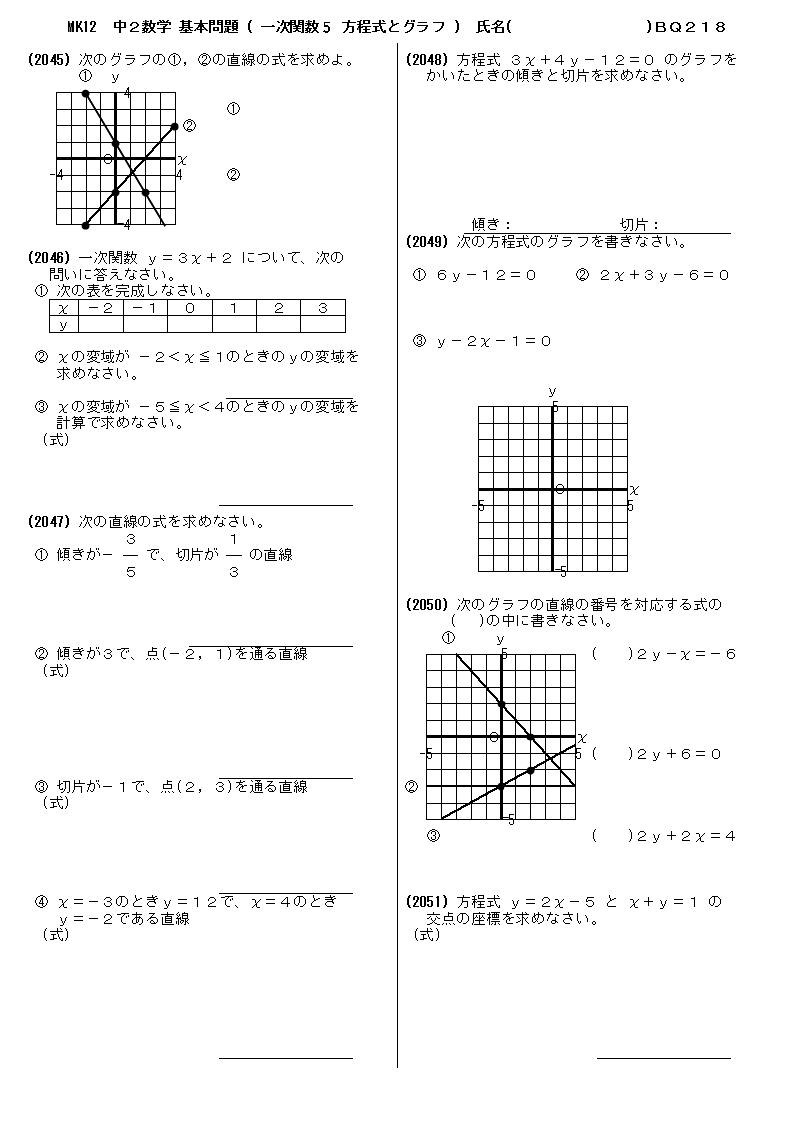



無料 中2数学 基本問題 問題プリント 218 一次関数6 方程式とグラフ




一次関数 Wikipedia



一次関数 グラフから式を求める方法について徹底解説 数スタ



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su



一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス




1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張



中2数学 一次関数と方程式 X Y グラフ Xが数字 Yが数字だけ の書き方 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




まる先生 一次方程式と二次方程式のグラフは どんどんかきこみをする まる練 自宅学習 家庭学習 テスト対策 テスト勉強 マンガで勉強 高校入試 高校受験 まる練数学 一次方程式 二次方程式 グラフ



中2 1次関数4



中学数学 1次関数 式からグラフへ 中学数学の無料オンライン学習サイトchu Su



1次関数のグラフのかき方 Youtube



一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス




数学 中2 35 二元一次方程式のグラフを書く Youtube
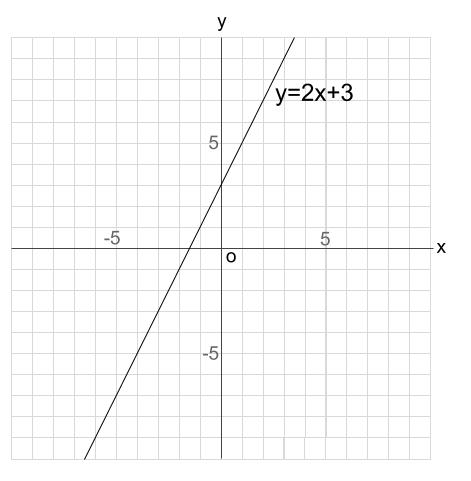



中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su
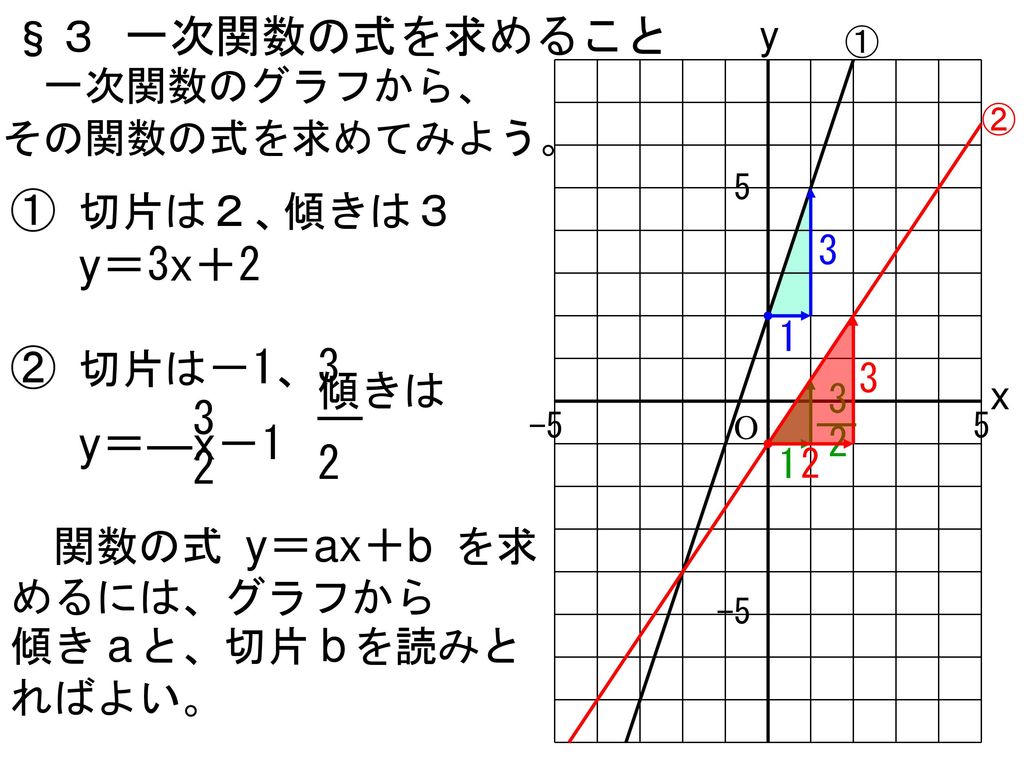



3 一次関数 1章 一次関数とグラフ 3 一次関数の式を求めること 3時間 Ppt Download
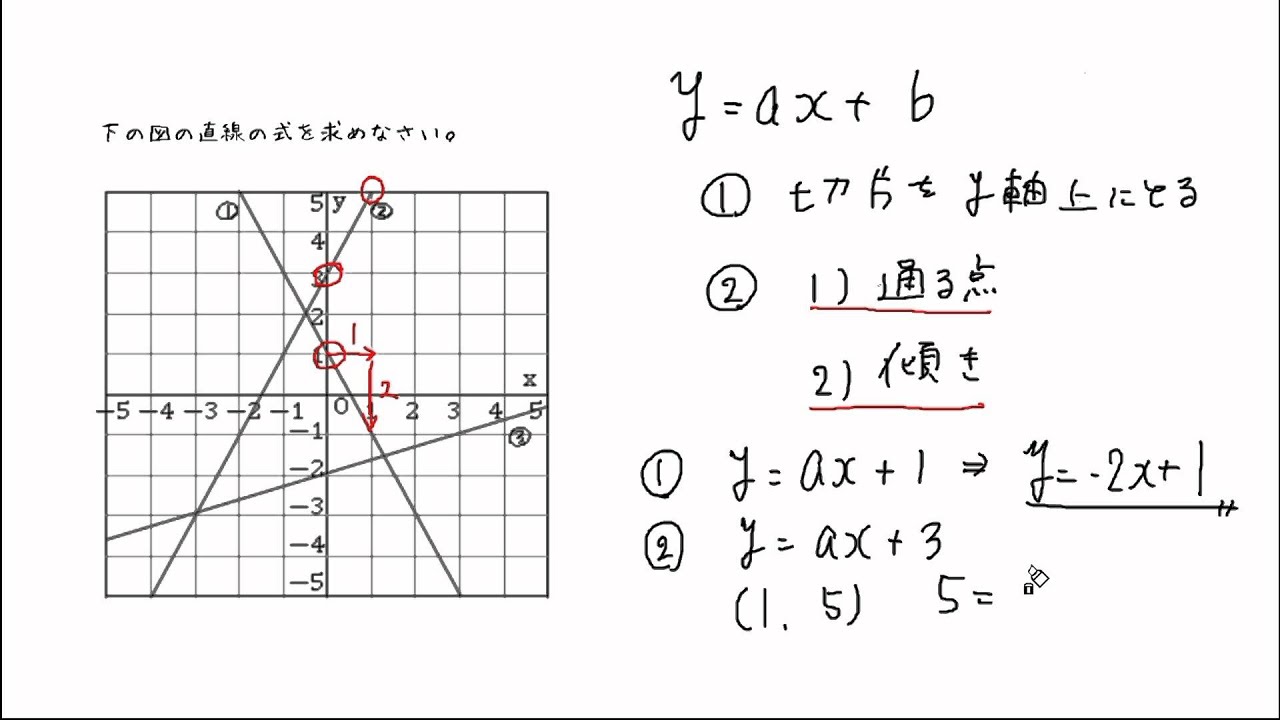



グラフから一次関数の式をもとめる Youtube
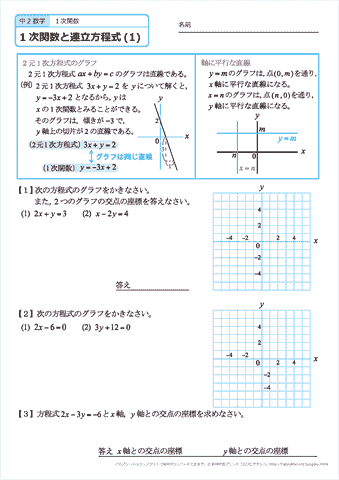



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
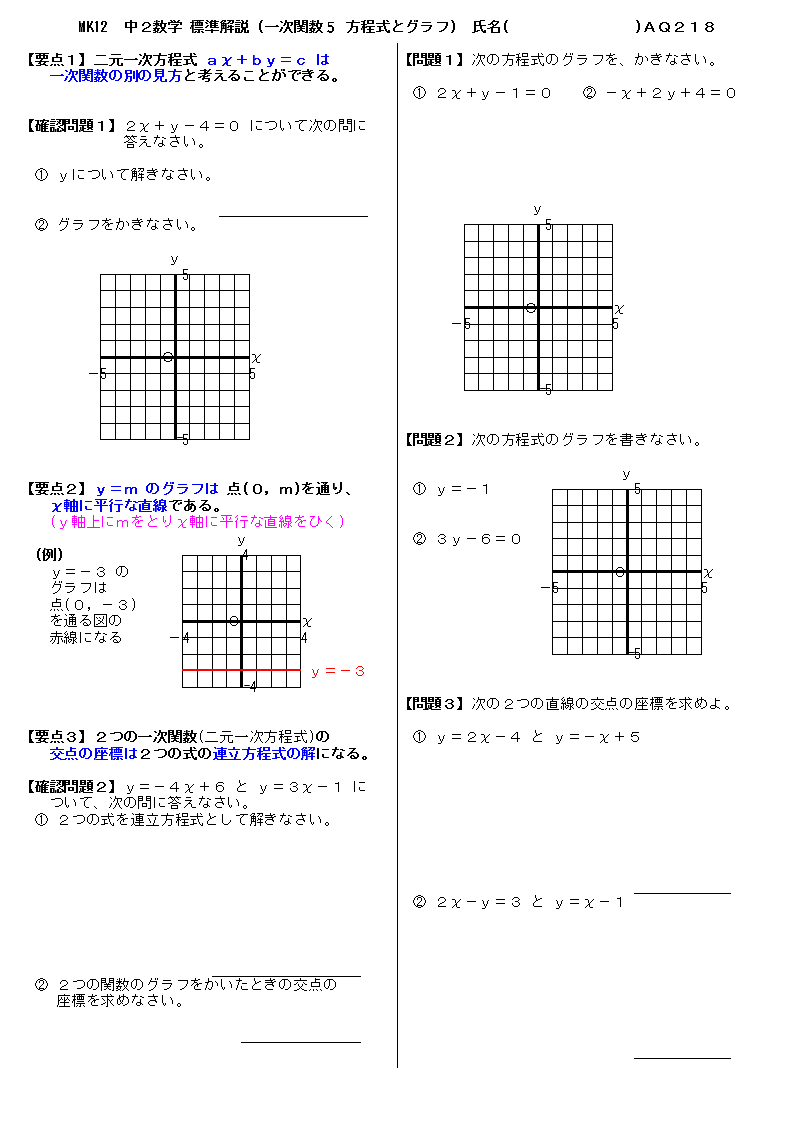



無料 中2数学 基本解説 問題プリント 218 一次関数6 方程式とグラフ




中2数学 1次関数のグラフの書き方 例題編 映像授業のtry It トライイット
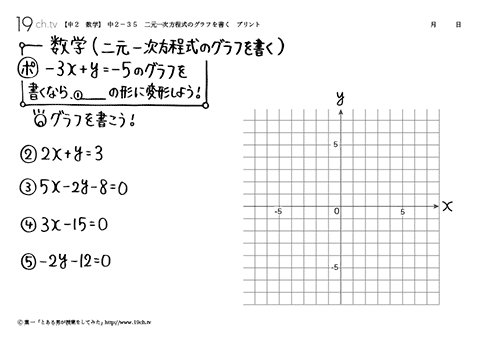



中学2年の数学 動画 二元一次方程式のグラフを書くの問題 19ch
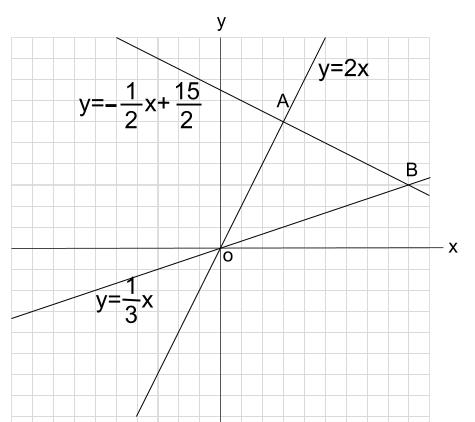



中学数学 1次関数と三角形の面積 その2 中学数学の無料オンライン学習サイトchu Su




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく




1次関数と2元1次方程式の違い Youtube



超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




中2数学 1次関数のグラフの書き方 例題編 映像授業のtry It トライイット



連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト




基本 一次不等式と一次関数のグラフ なかけんの数学ノート




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1



Sage Text 方程式の解法 Pukiwiki




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく



二限一次方程式のグラフについてです この問題を解くのにそれぞれx Yに0 Yahoo 知恵袋



中2数学 1次関数 連立方程式とグラフ オンライン無料塾 ターンナップ




Excelテクニック And Ms Office Recommended By Pc Training Excel Y 2x 一次元方程式のグラフ の作り方



一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download



一次関数の要点まとめ



Math 超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 働きアリ



1次関数の交点の座標とグラフから直線の方程式を求める方法



一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download



中三数学二次方程式の応用一次関数の利用グラフの問題が苦手です 下の Yahoo 知恵袋
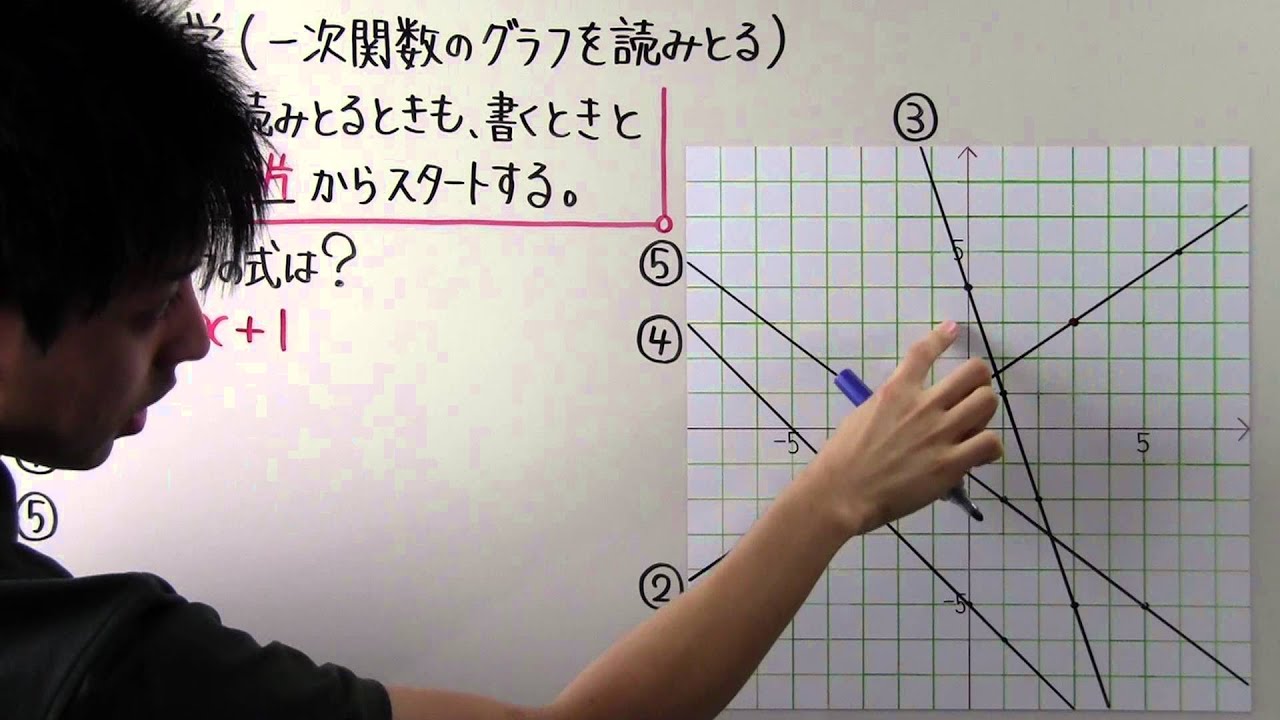



数学 中2 34 一次関数のグラフを読みとる Youtube




一次関数のグラフの利用1 無料で使える中学学習プリント




2元1次方程式とグラフの書き方 中2数学 Youtube



1
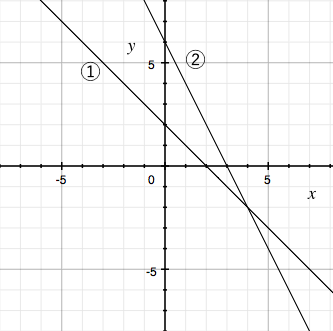



一次関数 連立方程式とグラフの関係 苦手な数学を簡単に




完全版 一次関数のグラフから利用問題まで解き方まとめ 中学数学 理科の学習まとめサイト
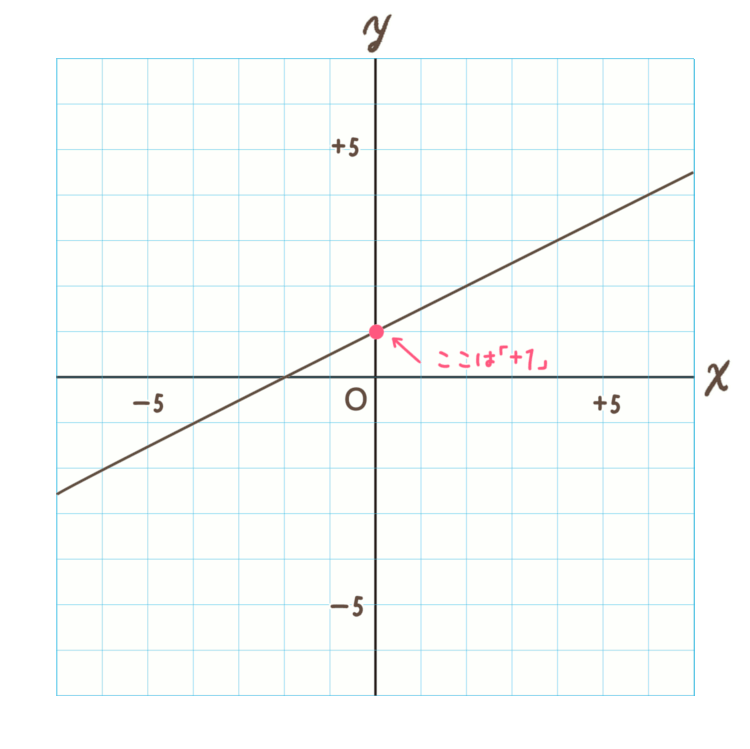



中2の数学 をバッチリ攻略 連立方程式や一次関数を解説 家庭教師ジャニアス
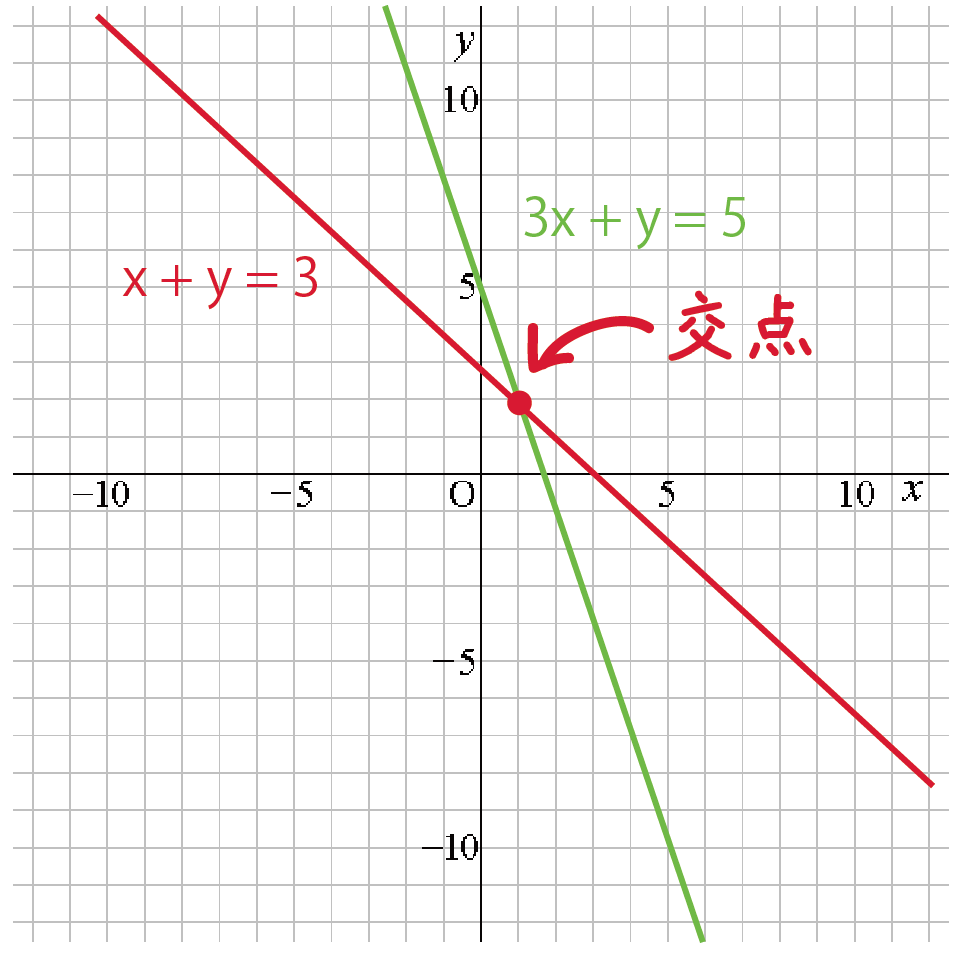



一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく
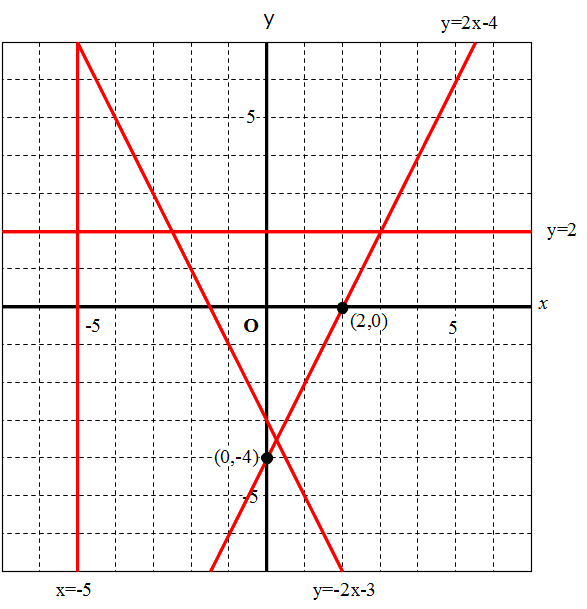



Math 超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 働きアリ




切片が分数の時どうやってグラフを書くのかがわかりません 教えて欲しいです Clear
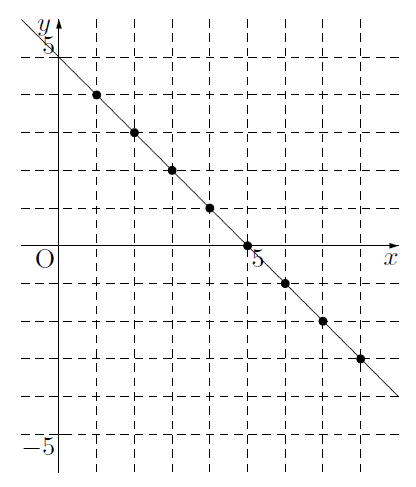



2元1次方程式のグラフ まなびの学園
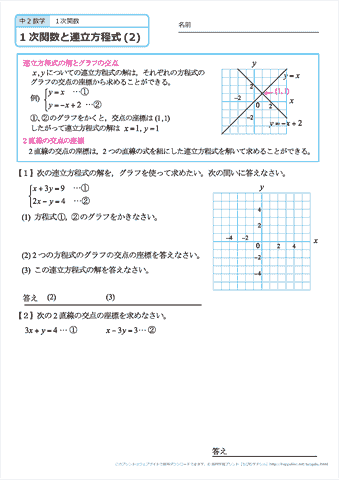



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
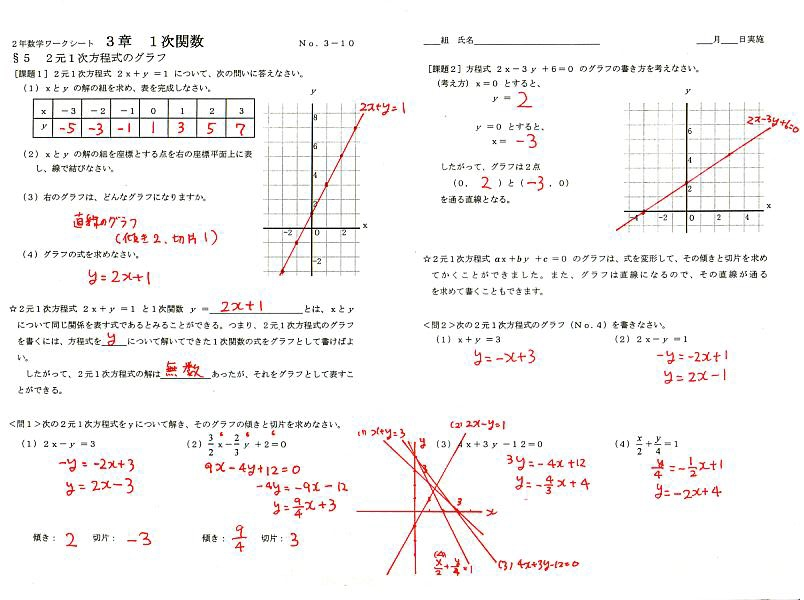



5 2元1次方程式のグラフ Mathweather4067のblog




Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア
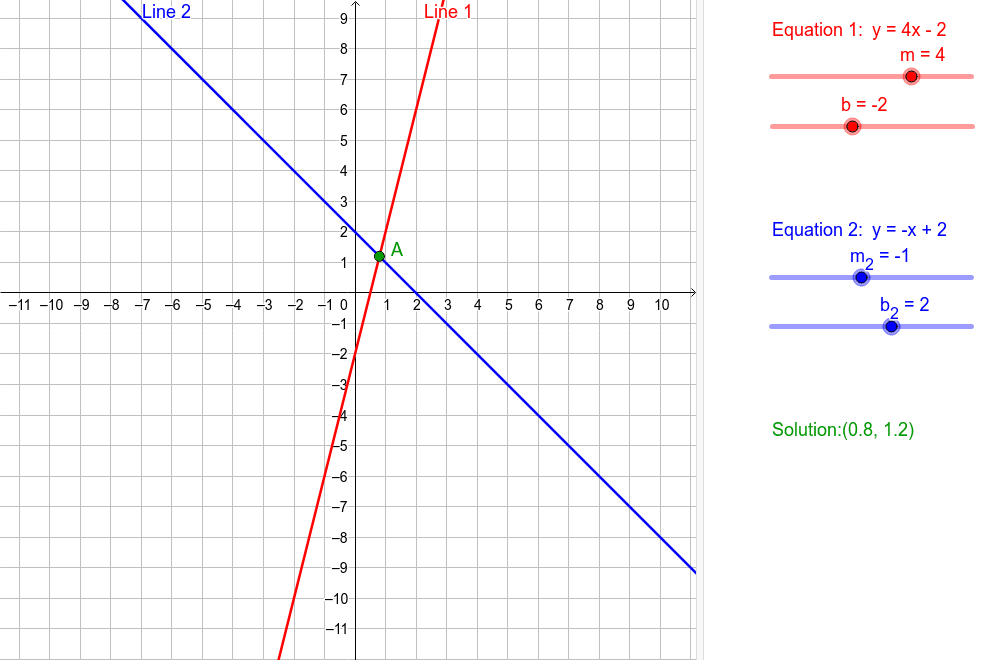



1次関数と方程式 Geogebra




X 3y 7の二元一次方程式 方程式のグラフ を教えてください Clear




方程式と関数の違いを理解しよう 理系のための備忘録
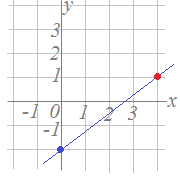



1次関数 グラフ 直線の方程式
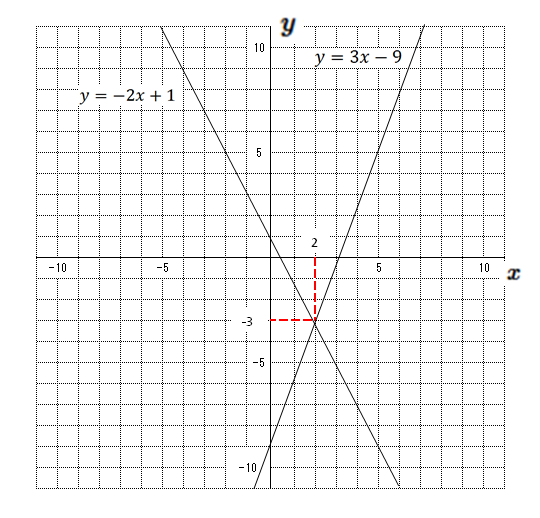



一次関数と連立方程式 1 ネット塾



0 件のコメント:
コメントを投稿